水理計算の基礎知識-11章
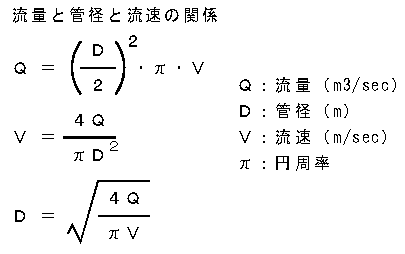
流量と管径と流速の関係
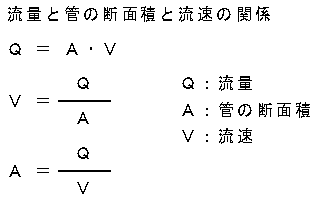
流量と管径と流速の関係
まず、流量と流速と管の断面積の関係は次式で表せます。
Q = A・V
Q:流量 A:管の断面積 V:流速
管の断面積は「半径×半径×円周率」で求められますので、新たに「D」を管径とした場合、「D / 2」で半径、「(D / 2)^2・π」で管の断面積となりますのでこれを上記式に代入すると、
Q = (D / 2)^2・π・V
Q:流量 D:管径 V:流速 π:円周率
となります。
この式をさらに流速を求める式にすると、
V = 4Q / πD^2
となり、流量が一定であるならば管径が大きくなると流速は小さくなり、管径が小さくなると流速は大きくなることが分かります。
流速はこのようにして、流量と管径から求めることができます。
そして水理計算の目的のひとつに所要水頭の算出がありますが、この所要水頭の算出も流量と管径を基にして行います。
ですから所要水頭を算出する際には、同時に流速も算出して、流速が2.0m/秒を超えないようにし、もし超えるようであれば管径を大きくして再度計算し、適切な管径を決定します。
流量と管の断面積と流速の関係をまとめたものが(図11-1)、流量と管径と流速の関係をまとめたものが(図11-2)です。
(図11-1)
(図11-2)